The Mid-point Theorem
The Mid-point Theorem: Overview
This topic covers concepts, such as, Mid Point Theorem in a Triangle, Mid Point Parallel Line Theorem in a Triangle & Mid Point Theorem in a Quadrilateral etc.
Important Questions on The Mid-point Theorem
In is the mid-point of median such that produced meets at . If , then .
If and are respectively the midpoints of the sides and of in which and then determine the length of .
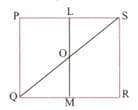
In Figure shown below, PQRS is a square. L and M are respectively, the mid points of PS and QR. Find the area of , if cm, and O is the point of intersection of LM and QS.
In a and are mid points of and respectively. Calculate
In a and are mid points of and respectively. Calculate
In a are mid points of sides and respectively. If cm then what is the length of ?
Prove that the triangle formed by joining the mid points of the sides of an isosceles triangle is also an isosceles triangle.
In given figure, and are respectively the mid-points of the opposite sides and of a parallelogram . and intersect at and respectively. Show that.
ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that area (DCYX) = area (XYBA).
ABC is a triangle whose area is . and are mid points of the sides and respectively. Prove that is a trapezium. Also find its area.
Show that the quadrilateral formed by joining the mid points of the adjacent sides of a square is also a square.
In any triangle ABC, prove that three times the sum of squares of its sides is equal to four times the sum of squares of its medians.
Show that the quadrilateral, formed by joining the mid-points of the consecutive sides of a rhombus is a rectangle.
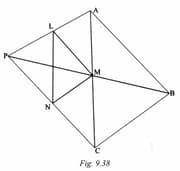
In Fig. from a point , straight lines of unequal lengths are, drawn. If are their mid points respectively, prove that are equiangular.
In a right angled triangle and is mid point of . Prove that
In a kite shaped figure Points are mid points of sides respectively. Prove that
line through and parallel to bisects side
In a kite shaped figure . Points are mid points of sides respectively. Prove that
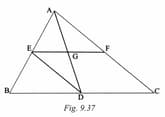
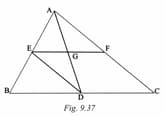
In Fig. is the mid point of the side of a A line through parallel to meets and a line through parallel to meets the median . Prove that
In Fig. is the mid point of the side of a A line through parallel to meets and a line through parallel to meets the median . Prove that